Genom tiderna har det funnits många olika typer av talsystem för att kunna genomföra olika beräkningar. Exempelvis mayafolkets talsystem eller romarrikets talsystem. Båda dessa talsystem var väldigt annorlunda jämfört med vårt talsystem som vi använder idag. Kommentera gärna på videon om du vill veta mer om dessa talsystem.
Vårt talsystem är ett så kallat positionssystem. Det innebär att vi med några få siffror kan skriva alla tal eftersom positionen som en siffra har bestämmer dess faktiska värde.
Positionssystem
Vårt talsystem har 10 siffror (0,1,2,3,4,5,6,7,8,9). Med dessa 10 siffror kan vi skriva alla tal som vi kan komma att tänka på. Eftersom vi använder oss av 10 siffror kallas det också ibland för tiobassystem eller tiosystemet.
Vad är ett positionssystem?
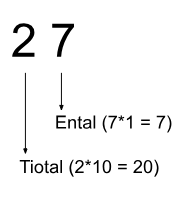
Enkelt förklarat så är olika bestämda positioner olika mycket värda. Antagligen har du hört talas om till exempel ett ental och tiotal. Detta är just kopplat till siffrornas positioner.
Skulle siffrorna istället byta plats i exemplet här ovanför skulle siffran 7 vara värd 70 och siffran 2 vara värd 2.
Andra positionssystem
Det finns även andra positionssystem använder både fler och färre siffror, t.ex. det binära talsystemet (ordet bi betyder 2). Där skriva man tal med endast 2 siffror, nämligen siffrorna 0 och 1 (2 siffror = bi). Det binära systemet fungerar så att positionernas värde hela tiden fördubblas. Har du till exempel det binära talet 10110 och vi skriver in det i en tabell för att lättare kunna se de olika positionerna värden ser du att vi har en etta vid värdena 16, 4 och 2. Lägger vi ihop dessa 16+4+2 får vi 22. Alltså är 10110 samma sak som talet 22 i vårt talsystem.
| Positionens värde | 16 (24) | 8 (23) | 4 (22) | 2 (21) | 1 (20) |
| Siffror | 1 | 0 | 1 | 1 | 0 |
Vårt talsystem
Tillbaka till vårt talsystem (tiosystemet). Det fungerar på samma sätt som det binära talsystemet men våra positioner har andra värden och vi kan ha fler än värdet 1 på de olika positionerna. Vi tar talet 1 243 som exempel.
| Positionens värde | Tusental (103) | Hundratal (102) | Tiotal (101) | Ental (100) |
| Siffror | 1 | 2 | 4 | 3 |
Tabellen visar från höger till vänster att det finns 3 ental (3*1= 3), 4 tiotal (4*10=40), 2 hundratal (2*100=200) och 1 tusental (1*1000=1000)
Lägger vi ihop dessa 1000+200+40+3 får vi just 1 243.
Heltal
Talet 1 243 är ett heltal. Alla tal som kan skrivas utan decimaltecken är heltal. T.ex är talet 1 och talet 42 heltal. Talet 6,5 är inte ett heltal eftersom det måste skrivas med ett decimaltecken. Heltal kan även vara negativa, alltså är även -1 och -42 heltal.
Decimaltal
Ibland behöver vi skriva tal som inte är heltal, det har vi också möjlighet att göra med vårt talsystem, så kallade decimaltal. Detta bygger, precis som tidigare, på att olika positioner har olika värden.
| Tusental (103) | Hundrata (102) | Tiotal (101) | Ental (100) | , | Tiondel (10-1) | Hundradel (10-2) | Tusendel (10-3) |
| 1 | 2 | 4 | 3 | , | 5 | 2 | 2 |
Decimaltal är ett sätt för att beskriva tal som inte är hela. Exempelvis är talet 0,5 inte 0 och inte heller 1 utan precis mitt emellan 0 och 1.
Heltalet 1 kan delas upp i 10 st tiondelar eller 100 st hundradelar eller o.s.v
Heltalet 2 kan delas upp i 20 st tiondelar eller 200 st hundradelar eller o.s.v
Hur många tiondelar består då talet 1,2 av? Jo, en hel består av 10 st tiondelar och sedan ser vi att talet även har en 2:a på tiondelspositionen och består därför av ytterligare 2 tiondelar. Alltså består talet 1,2 av 10 + 2 tiondelar som är 12 tiondelar.
Andra typer av tal
Naturliga tal: Är tal som du kan räkna till genom att lägga ihop stenar eller annat. Alltså fysiska saker. De naturliga talen börjar med talet 0 (som varken är positivt eller negativt) och fortsätter sedan med större och större tal.
Negativa tal: Tal som är mindre än 0 kalla för negativa tal. Oftersom 0 varken räknas som ett positivt eller ett negativt tal börjar de negativa talen med -1 och fortsätter med mindre och mindre tal.
Reella tal: Alla tal som går att placera ut på en tallinje kallas för reella tal, eftersom både heltal och decimaltal går att placera på en tallinje räknas de som reella tal. Även bråktal räknas som reella tal.
Fundera på!
Om du fick gissa, hur många tal tror du att vi kan skriva med vårt talsystem?
Svaret på den frågan är att vi kan skriva oändligt många tal med vårt talsystem, vi kan alltid skriva större och större tal och vi kan alltid “klämma in” tal mellan två befintliga tal så det finns egentligen inget slut på mängden tal vi kan skriva.
Tänk dig en linjal. Linjalen är 30 cm lång. Om vi väljer att titta på siffrorna mellan 0 och 10 så kan vi se att det är just 0-10 där. Om vi nu tittar närmare på endast denna del av linjalen så kan vi se att det även finns fler “streck” som delar in dessa delar, våra millimeter. Vi kan välja att nu istället titta på avståndet mellan 3 och 4 på linjalen och då ser vi att det är 10 streck där. T.ex kan du se 3,4. Ett tal som alltså är större än 3 men mindre än fyra. Om du åter igen tänker dig att du tittar på avståndet mellan två av millimeterstrecken på linjalen och zoomar in så att allt förstoras så kan du åter igen se att vi kan placera in tal mellan t.ex. 3,4 och 3,5. Då hittar du kanske ta.et 3,47.
Vi skulle kunna hålla på så här hur länga som helst, vi får bara tal med fler och fler decimaler vilket innebär att vi faktiskt kan skriva oändligt med tal med vårt talsystem. Vilket är bra eftersom det faktiskt finns oändligt med tal runtomkring oss.
Comments are closed